八字型几何例题,八字型几何规律
八字型几何例题,八字型几何规律

几何学是数学的一个重要分支,研究空间中的形状、大小、位置关系等问题。其中,八字型几何是一种特殊的几何形状,具有独特的规律和特点。本文将以八字型几何例题为中心,探讨八字型几何的规律。
例题一:求八字型的面积
已知八字型的上下边长分别为a和b,左右边长分别为c和d。求八字型的面积。
解:八字型可以分解为两个矩形和两个半圆组成。上下两个矩形的面积分别为a*b和c*d,两个半圆的面积分别为(1/2)*π*(a/2)^2和(1/2)*π*(c/2)^2。八字型的面积等于两个矩形的面积之和加上两个半圆的面积之和,即S = a*b + c*d + (1/2)*π*(a/2)^2 + (1/2)*π*(c/2)^2。
例题二:八字型的对称性
八字型具有对称性,即左右对称和上下对称。
左右对称:八字型的左边和右边的边长相等,且平行。这意味着八字型关于垂直中轴线对称。
上下对称:八字型的上边和下边的边长相等,且平行。这意味着八字型关于水平中轴线对称。
例题三:八字型的相似性
八字型具有相似性,即可以通过缩放比例得到相似的八字型。
设原八字型的边长为a、b、c、d,缩放比例为k,则相似的八字型的边长为ka、kb、kc、kd。
相似的八字型的面积和原八字型的面积之比为k^2。
例题四:八字型的特殊性质
八字型的特殊性质包括:对角线相等、内角和为360度。
对角线相等:八字型的对角线AC和BD相等。
内角和为360度:八字型的内角和为360度,即∠A + ∠B + ∠C + ∠D = 360度。
通过以上例题和规律的分析,我们可以更好地理解八字型几何的特点和规律,为解决和应用相关问题提供了基础。
八字型几何是几何学中的一个重要概念,具有独特的规律和特点。通过解题和分析,我们可以更好地理解八字型几何的性质和应用,为解决相关问题提供了基础。
发布于 2024-11-17 16:36相关推荐
-
八字年月地支相同规律
“八字年月地支相同规律”这一古老的命理学理论,自古就流传至今,并被视为一种准确预测未来的科学。据说,..
-

12什么星座 12星座中谁生活方式最有规律
12什么星座 12星座中谁生活方式最有规律在12星座中,每个星座都有其独特的性格和生活方式。有些星座倾向于..
-
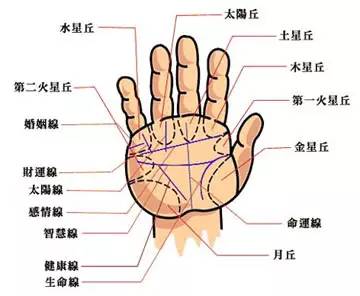
手相看健康,九体质的手诊规律
手相(英文:palm)其源有西洋、印度和中国三支,源远而流长,终成今日博杂大观。用手相手型与手纹来判断一生..
-
八字形模型例题
八字形模型是一个有关于人生方向和性格特点的分析模型。在这个模型中,根据一个人的生辰八字来判断他的五行..
-

发现一些奇怪但必须相信的恋爱规律: 1. 当你不在...
发现一些奇怪但必须相信的恋爱规律:1. 当你不在意感情,真正专注于自己时,缘分就会来敲门。当你不再想复..
-

彩票真是“智商税”吗?中奖真的有规律吗?值不值得一试
彩票,曾经是国人热衷于购买的一种游戏,既寄托了中奖的梦想,也被有些人嘲讽为“智商税”。然而,对于彩票..
-

梦见攻读法律、学习法律什么意思
梦到攻读法律、学习法律法律是人们给行为所定下的必须遵守的法律准则。梦中,法律代表着社会的世俗规律。而..
-

是儿是女,财气如何,长寿几何,要看这些定数
在古老的中华文明中,人们一直对生辰八字怀有敬畏之情。这种远古的算命术,包括对儿女、财富、寿命的预测,..
-

双色球第96期分析,阶段性规律探讨,24、26、33可能出现。
彩友同仁,大家上午好!今天8月20日,农历7月17丙辰日,五行纳音为沙中土。沙中土五行缺木,也就是尾数是4..
-

大明星算命
“明星”的英语是Star。单词解析:英 [stɑ:(r)]美 [stɑr]n.星星;星星;星星;星星v.主演;(文字等)标星..
-

五行相生相克的规律
在五行中,有相互制约、相互克服的关系,这种关系称为“相互克服”。五行的规律是:木克土、土克水、水克火..
-

周易数理吉凶理论
中国古代术数排名什么是术数呢?《辞海》有云,术数以种种方术观测自然界可注意的现象,来推测人和国家的气..
-

崔姓男宝宝起名大气
自古以来,给孩子取名就是一件非常重要的事情。崔姓是百姓之一。崔的名字有很多非常合适的名字,但并不是所..
-

测算名字免费,周易起名网唯一官网免费
提到免费计算名称和命运,我们都知道,有些人问免费计算名称的好坏,包括对自己的一些期望,我们有点随意,..
-

不得不看的十个玄学规律,推给有缘人
-

五运六气吉凶原理是什么
人生的起伏往往伴随着五运六气的转变,这是中国传统文化命运变化的重要理论之一。五运是指金、木、水、火、..
-

星云算命
星云算命星云算命是一种古老的占卜方法,它起源于传统文化,通过观察天体的运行规律来预测未来的命运。这种..
-

松赞干布究竟寿禄几何?是八十二,还是三十四?
松赞干布作为西藏历史最辉煌时代的缔造者,历史地位堪称藏史一哥。正是因其无与伦比的影响力,他究竟寿禄几..
-

四柱八字解析有科学道理吗
众所周知,有人问四柱八字命理详解,有人想问四柱八字排盘详解。你知道发生了什么吗?其实生日八字分析,我..
-

如何学算命精准预测
精通算命:提高预测精度的秘诀掌握算命并准确预测未来并不容易。然而,遵循一些关键的原则和实践,你可以大..
-
为什么正月的羊不好 生肖羊几月生最好
我们每个人都会有不同的命运,而我们的命运如何除了通过自己的经历来看以外就是通过我们的出生时间来看了,很多人都说正月出生的生肖羊命运比较不好。那么今天我们一起来看看为什么正月的羊不好?生肖羊几月生最好?..
点赞2026-02-26 15:56 -
天秤女喜欢一个人的表现
天秤座的女生在确定了自己的爱情是纯洁之后才会真心喜欢对方,而且天秤座女生喜欢的男生也会有时候觉得天秤女会问一些奇怪的问题,对此天秤女喜欢一个人的表现是怎样的呢?下面一起来看看吧。 天秤女喜欢一个人的表..
点赞2026-02-26 15:48 -
属龙十月生女命好不好 龙女十月哪天生好
龙女对自己很自信,她们很少为了显出自己的尊贵而过度装扮,她们天生丽质难自弃,无需装扮的人也会让人觉得自己很有魅力。她们是非常勇敢,并且满是自信,是一个敢于冒险,敢于奋斗的女孩。那么属龙十月生女命好不好..
点赞2026-02-26 15:44 -
中国传统民俗文化有哪些
中华文化源远流长,历史悠久。自古以来,我国的传统民俗文化便一直在人民生活中扮演着不可或缺的角色。每个节日,每个场合都有其自己独特的风俗习惯和文化内涵。今天,本文就带您一起了解一下中国的传统民俗文化。中..
点赞2026-02-26 15:37 -
摩羯座女爱情
摩羯座的人是在十二星座里面最有耐心与爱心的一个星座,那么你知道摩羯座女爱情是怎样的吗?下面我们就来看看以下文章吧!摩羯座女爱情 摩羯座女生的爱情 摩羯座的女生:忠心耿耿,日久必生情。 摩羯座的你常常会不..
点赞2026-02-26 15:37 -
属马的年份 出生在不同年份的属马人运势
属马的年份是哪几年呢?生肖纪年法是按照中国传统的干支历法的,不等同于公历年,但是大致却是相对的。生肖马才华横溢的,他们生性好动却爱出风头,那么,出生在不同年份的属马人运势如何呢?了解更多生肖运势,就来..
点赞2026-02-26 15:31 -
属狗天蝎座男生特点
天蝎座是在十二星座里面排行第八的,你知道属狗天蝎座男生特点是怎样的吗?下面我们就来看看以下文章吧!属狗天蝎座男生特点 属狗天蝎座男生性格特点 属狗的天蝎座,不知道为什么,在所有的星座与生肖比例组合中,这..
点赞2026-02-26 15:27 -
五行火字最旺的字取名
1、八字属火的字八字是中国传统文化中的一种算命方法,通过分析个人的出生年、月、日、时的八个字,来推算出一个人的命运和性格特点。其中,属火的八字具有独特的意义和影响。如果你的八字属火,代表你的性格活泼开..
点赞2026-02-26 15:26 -
农历四月属牛男好吗 农历四月牛和谁最配
属牛的男人脚踏实地,按部就班,稳扎稳打,出了名的谨慎。也因此,属牛的男人多为事业成功男士,其坚韧不拔的毅力不是一般人所能比拟。而单纯的属牛男性在感情可能不会甜言蜜语,不会不择手段的去获得自己的恋情。那..
点赞2026-02-26 15:20 -
天蝎男喜欢一个人的表现
天蝎座的男生喜欢一个女生的话,那么就会找一个真正让自己心动的女生。而且不会找一些不是真爱的感情,对此天蝎男喜欢一个人的表现到底是怎样的呢?下面一起来看看吧。 天蝎男喜欢一个人的表现 天蝎座男生喜欢一个人..
点赞2026-02-26 15:14 -
八字里的印劫是什么意思
1、八字里的印八字学是中华文化的重要组成部分,它是根据出生时的年、月、日、时辰,排列成的八个字所代表的天时地利来推算命运的学问。其中,印是八字中重要的元素之一,是代表着个性与才华的表现,在命理学中被认..
点赞2026-02-26 15:13 -
属蛇出生时辰命运最好 哪年出生的属蛇人最好命
蛇给人的印象不佳,有阴险狡滑的习性,行动闪烁,不光明正大。因为在十二地支中,巳和午都属火,午的人更旺,巳的人较不热,属阴性之火,所以蛇年 之人,内心明亮温暖,是个适合从事精神层次活动的人,也具有向上心..
点赞2026-02-26 15:10 -
八字影壁墙的做法
在中国传统文化中,八字是非常重要的一种命理学要素,它由人的出生年、月、日、时组成,据此可以推算出一个人的各种命理属性。而八字影壁墙则是对八字的一种表现形式,它可以通过一系列的手工制作工艺来展示出一个人..
点赞2026-02-26 15:00 -
属羊考科目四难吗 好不好
属羊考科目四难吗?科目四的题目数量虽然少于科目一,但是科目四的题目类型比科目一要复杂,除了单选还有多选,记忆难度更大。那么属羊考科目四好不好呢?考试运势如何呢?科目四对服装有什么要求吗?了解更多生肖运..
点赞2026-02-26 14:58 -
1924年屋上之鼠命运怎么样 最享福的鼠是几月
在不同年份出生的人,所属的生肖也是不一样的。不过,十二年一轮,生肖又会重新来一次排序。但不在同一年出生的相同属相的人,生肖所拥有的命运也是有差别的。那么,对于出生在1924年的屋上之鼠来说,会有怎样的命运..
点赞2026-02-26 14:46 -
有硅胶的八字环
“有硅胶的八字环”:萌萌哒的时尚小物品没有人能够否认时尚小物品对于我们的日常生活中的重要性。今天,我想要谈论的是一种独特而迷人的时尚小物品——有硅胶的八字环。这个小小的物品被越来越多的人所接受和喜欢,..
点赞2026-02-26 14:46 -
卓字取名的寓意
父母为孩子起名,常精挑细选,那卓字取名的寓意是什么呢?卓字取名的寓意。卓字,五行属性为火,本义为高超、高明;寓意为优异出众;用作人名则有追求完美之义。取名为卓姝姝字,五行属性为金,金可生水,属鼠、属猪..
点赞2026-02-26 14:35 -
高强轴承环八字环
在机械中,高强轴承环八字环是一种重要的零部件。它具有稳定的形状和优良的性能,在解决轴承过紧或过松的问题上起到非常重要的作用。下面,我们将从材料、工艺、应用等多方面详细介绍高强轴承环八字环的相关知识。一..
点赞2026-02-26 14:34 -
1988年属龙7月出生的是什么命 88年属龙人三大坎
每一个人的命运从来都是不一样的。在命理学里,出生时间的差别限制了人们未来的人生道路。所以人各有命,不必羡慕别人有好命。那么对于出生在1988年7月的属龙人来说,会有什么样的命运呢?接下来就让我们一起带着这..
点赞2026-02-26 14:33 -
长八字胡子是好是坏
1、长八字胡长八字胡是一种非常独特的胡须风格,其特点是将胡须留得极长,形成类似于八字形状的造型。这种风格胡须既威严又狂野,常常被用来表现男性的不羁和个性。长八字胡的历史可以追溯到几百年前,当时这种胡须..
点赞2026-02-26 14:22
微信分享
扫描二维码分享到微信或朋友圈
